问题:如何经过convTransposed1d输出指定大小的特征?
import torch from torch import nn import torch.nn.functional as F conv1 = nn.Conv1d(1, 2, 3, padding=1) conv2 = nn.Conv1d(in_channels=2, out_channels=4, kernel_size=3, padding=1) #转置卷积 dconv1 = nn.ConvTranspose1d(4, 1, kernel_size=3, stride=2, padding=1, output_padding=1) x = torch.randn(16, 1, 8) print(x.size()) x1 = conv1(x) x2 = conv2(x1) print(x2.size()) x3 = dconv1(x2) print(x3.size()) ''' torch.Size([16, 1, 8]) torch.Size([16, 4, 8]) #conv2输出特征图大小 torch.Size([16, 1, 16]) #转置卷积输出特征图大小 ''' 计算转置卷积输出特征大小公式
输入:
(
N
,
C
i
n
,
L
i
n
)
(N, C_{in}, L_{in})
(N,Cin,Lin)
输出:
(
N
,
C
o
u
t
,
L
o
u
t
)
(N, C_{out}, L_{out})
(N,Cout,Lout)
计算
L
o
u
t
L_{out}
Lout大小:
L
o
u
t
=
(
L
i
n
−
1
)
×
s
t
r
i
d
e
−
2
×
p
a
d
d
i
n
g
+
d
i
l
a
t
i
o
n
×
(
k
e
r
n
e
l
s
i
z
e
−
1
)
+
o
u
t
p
u
t
p
a
d
d
i
n
g
+
1
L_{out}=(L_{in}-1)×stride-2×padding+dilation×(kernelsize-1)+outputpadding+1
Lout=(Lin−1)×stride−2×padding+dilation×(kernelsize−1)+outputpadding+1
dilation默认为1, 上式简写为:
L
o
u
t
=
(
L
i
n
−
1
)
×
s
t
r
i
d
e
−
2
×
p
a
d
d
i
n
g
+
k
e
r
n
e
l
s
i
z
e
+
o
u
t
p
u
t
p
a
d
d
i
n
g
L_{out}=(L_{in}-1)×stride-2×padding+kernelsize+outputpadding
Lout=(Lin−1)×stride−2×padding+kernelsize+outputpadding
kernel_size固定,由stride, padding, outputpadding共同决定输出特征大小。
问题:输出特定的
L
o
u
t
L_{out}
Lout大小
假如
L
i
n
=
8
,
L
o
u
t
=
23
,
k
e
r
n
e
l
s
i
z
e
=
3
,
o
u
t
p
u
t
p
a
d
d
i
n
g
=
1
L_{in}=8,L_{out}=23,kernelsize=3,outputpadding=1
Lin=8,Lout=23,kernelsize=3,outputpadding=1,根据上式可以求得:
s
t
r
i
d
e
=
3
,
p
a
d
d
i
n
g
=
1
stride=3,padding=1
stride=3,padding=1
#转置卷积 dconv1 = nn.ConvTranspose1d(1, 1, kernel_size=3, stride=3, padding=1, output_padding=1) x = torch.randn(16, 1, 8) print(x.size()) #torch.Size([16, 1, 23]) x3 = dconv1(x) print(x3.size()) #torch.Size([16, 1, 23]) 下面两图为演示conv1d,在padding和不padding下的输出特征图大小
不带padding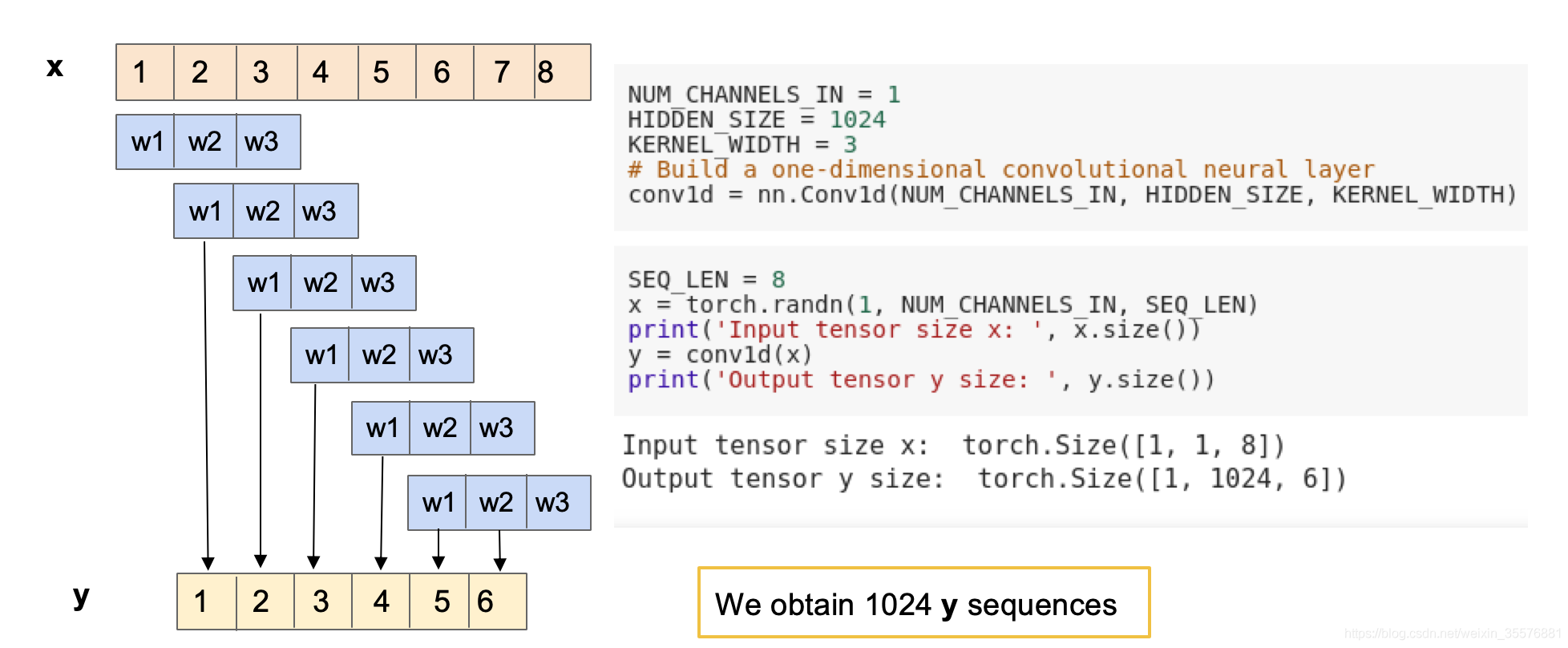
带padding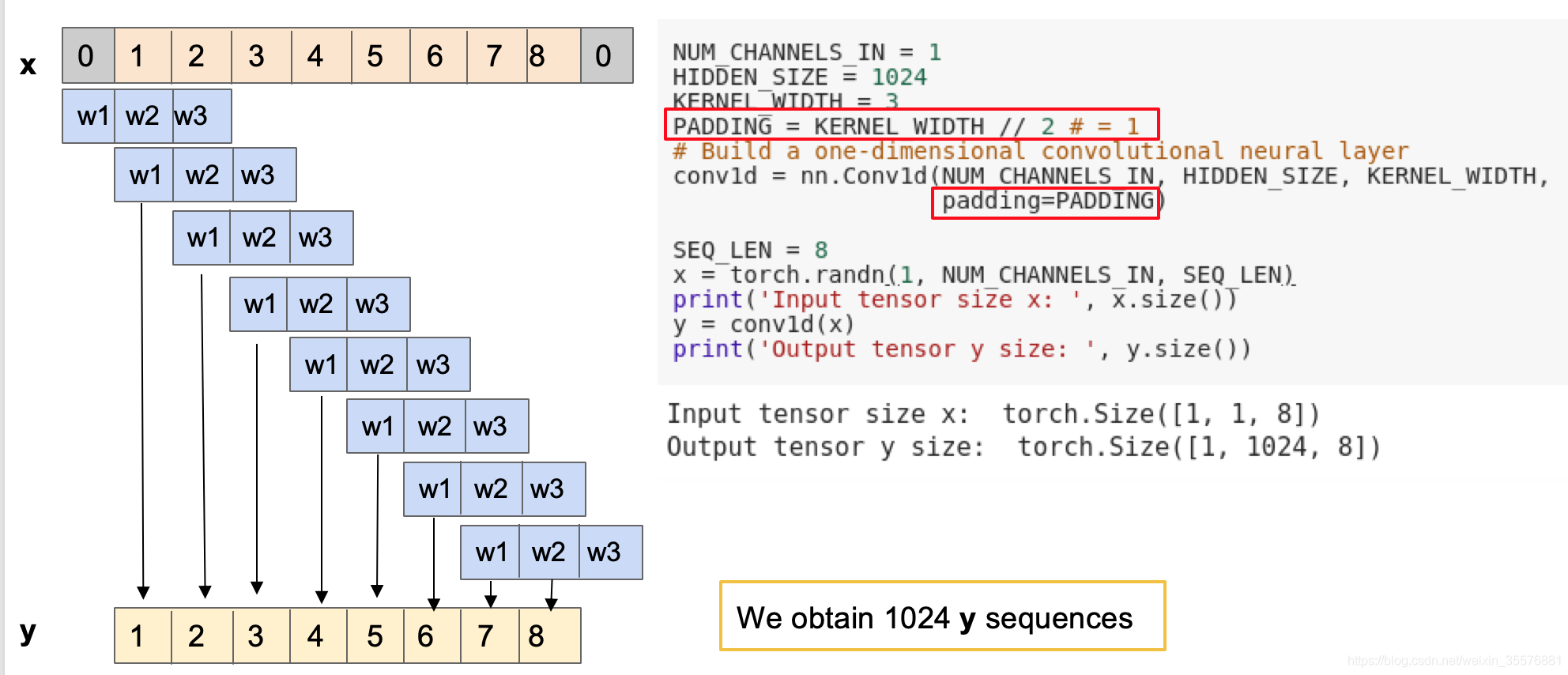
热门文章
- springboot整合Dubbo与Feign的实现 (无注册中心)_java
- 「3月25日」最高速度20.6M/S,2025年Clsah Verge每天更新免费节点订阅地址
- Mac上解决dose not contain the JNI_CreateJavaVM symbol
- 生产动物疫苗的上市公司有哪些 生产动物疫苗的上市公司有哪些股票
- 被猫咬伤怎么知道有没有病(被猫咬伤怎么知道有没有病毒感染)
- 「3月8日」最高速度20.9M/S,2025年Clsah Verge每天更新免费节点订阅地址
- 济南宠物狗领养中心地址在哪里(济南宠物领养济南宠物赠送)
- 「3月28日」最高速度19.1M/S,2025年Clsah Verge每天更新免费节点订阅地址
- 兽医门诊起名大全(兽医公司好听的名字)
- 属马人养猫能赚钱吗(属马人养猫能赚钱吗为什么)